De numeriska tecknen som vi vanligtvis använder när vi skriver har ett helt annat ursprung än alfabetet. Deras föregångare uppfanns i Indien under de första århundradena e.Kr. De togs i bruk av arabiska matematiker och köpmän som förde med dem till Europa under medeltiden. Därför kallas siffertecknen ibland indo-arabiska siffror.
I modern typografi finns det huvudsakligen två typer av siffror att välja mellan: versala siffror och gemena siffror. Siffrorna kan dessutom finnas i två olika bredder: proportionerlig bredd och fast bredd. Alla dessa alternativ har olika funktion i sättningen av böcker.
Versala siffror
Versala siffror har samma höjd som versala bokstäver. Med andra ord linjerar de med versala bokstäver på baslinjen och H-höjden.

Versala siffror är lämpliga att använda tillsammans med versaler. Att de följer samma linjer innebär att de harmoniserar med texten och inte bryter av.
När de används i kombination med gemena bokstäver sticker de konsekvent upp ovanför x-höjden och kan dra oönskad uppmärksamhet till sig. Effekten blir densamma som när man skriver ett ord med VERSALA bokstäver i brödtexten.
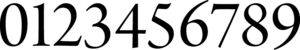
Många typsnitt som följer med i våra datorer, till exempel Arial, Calibri och Times New Roman, har enbart versala siffror.
Gemena siffror
Gemena siffror varierar i höjd på samma sätt som gemena bokstäver gör det:
- De kan hålla sig mellan baslinjen och x-höjden: 012.
- De kan sticka upp ovanför x-höjden: 68.
- De kan hänga ner under baslinjen: 34579.
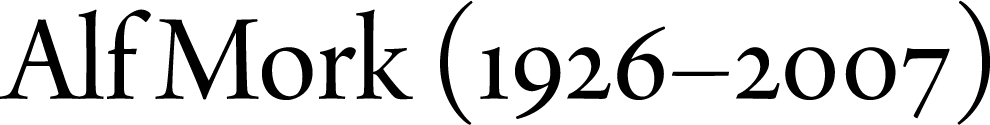
Gemena siffror används med fördel i de flesta sammanhang där gemena bokstäver är vanliga, exempelvis i romaners och fackböckers brödtext. De fungerar också bra i kombination med kapitäler, som har ungefär samma x-höjd som gemener. Tillsammans med versal text kan det däremot bli störande med de gemena siffrornas varierande höjd.
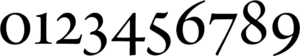
En del av de typsnitt som följer med våra datorer, exempelvis Candara, Constantia och Georgia, har enbart gemena siffror. Äldre Windows-datorer inkluderade oftast bara typsnitt med versala siffror. Av det skälet är versala siffror antagligen den sort som är mest välbekant hos allmänheten.
Proportionerlig bredd och fast bredd
Siffror med proportionerlig bredd har ungefär samma höger- och vänstermarginaler. Det totala utrymmet för varje siffra varierar då beroende på hur stort tecknet är. Detta är egentligen det naturliga. Proportionerlig bredd innebär att mängden vitt är jämnt fördelat runt siffrorna, och det uppstår inga distraherande fläckar eller luckor i läsningen.
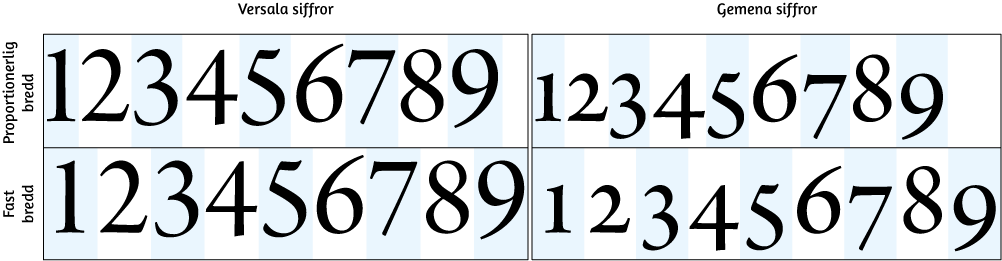
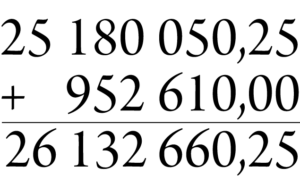
När alla siffertecknen har samma bredd kallas det att de har fast bredd. Fast bredd är praktiskt när siffror används i ekvationer, uträkningar eller tabeller. När siffrorna är lika breda är det lätt att se vilka tal som är störst, och vill man själv summera uppställningar blir det enklare när de olika värdepositionerna linjerar. Siffror med fast bredd bör dock undvikas i andra sammanhang, exempelvis i brödtext, då de tenderar att stå glest och därmed drar uppmärksamhet till sig. Effekten motsvarar den som uppstår när man s p ä r r a r gemena bokstäver.
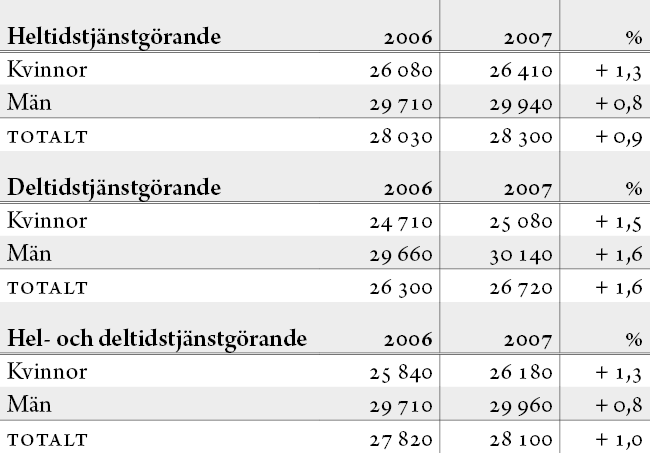
I ekvationer kan versala siffror med fast bredd vara att föredra framför gemena siffror, då de gemenas varierande höjd kan ge ekvationerna ett oroligt intryck. I större tabeller, där man vill vara så inbjudande som möjligt, kan det däremot vara lämpligt med gemena siffror som har en lite mjukare och vänligare framtoning.
De flesta siffror är normalt ungefär lika breda. Det krävs ofta ganska små justeringar för att de ska få samma bredd. Undantaget är siffran 1, som i regel är betydligt smalare än övriga siffror. I en del typsnitt får siffran 1 en extra bred seriff när den har fast bredd. Syftet är att bättre fylla ut utrymmet.
Slutsats
De tio tecknen som utgör våra siffror kan tyckas okomplicerade att ha att göra med. Men i moderna typsnitt finns en arsenal med olika alternativ för hur siffror och tal ska sättas. En erfaren boktypograf vet när det är lämpligt med versala siffror och när gemena är att föredra, eller i vilka sammanhang fast bredd fungerar bättre än proportionerlig. Rätt val av siffertecken kan förvandla skrikiga tal till diskreta, och göra de mest oöverskådliga tabeller till en fröjd för ögat.